The life of pi

The life of pi, [See "Later note" below] The Independent, 13 March 2006, Steve Connor ... The United States accords pi the ultimate accolade tomorrow, its own national day, charts its history and celebrates a number that is irrational, transcendental ... and unique. In case it has escaped your attention, tomorrow is 14 March which, in American notation, is written 3/14. If you have a certain type of mind you will immediately notice that these digits bear a close approximation to one of the most important numbers in mathematics - pi. Tomorrow has therefore been declared World Pi Day in honour of the mathematical constant that has beguiled and bewildered successive generations of numerate scholars since the days of ancient Babylon. Every schoolchild is told pi is the ratio of the circumference of a circle to its diameter. In other words, divide the distance around the edge of a circle by its diameter and you always get the same or "constant" number - pi. It's a nice bit of trigonometry that we learn by gradual osmosis and forget by rapid diffusion. Yet its simple truth has provided mathematicians - ancient and modern - with a cornucopia of conundrums. The first and most interesting is working out the precise value of pi. That has proved something of a challenge since the decimal places of pi can theoretically run on for ever. .. A supercomputer in Tokyo once calculated pi to more than 2 billion digits. It could not, however, reach the final decimal place because as every mathematician knows, that lies somewhere beyond infinity, a place they go only in their dreams. ... A less exact value was given by another early reference to pi, this time in the Bible (Kings 7:23), which described a round basin with the dimensions: 10 cubits in diameter and 30 cubits in circumference. Scholars point out that, although this gives us a neat and tidy value to pi of exactly three, it is unfortunately quite inaccurate ... It was however Archimedes who is credited as being the first to elevate the calculation of pi to a more theoretical discipline. It is for that reason the number is sometimes known as Archimedes' constant. . If William Jones, a Welsh mathematician, is remembered for one thing it is his suggestion to call Archimedes's constant "pi" after the Greek letter. ... In 1761, Johann Lambert demonstrated the irrational nature of pi. In its simplest terms, that meant you could not describe the number as a simple ratio of two whole numbers. ... The second major discovery came in 1882 when Ferdinand von Lindemann proved that pi had another unusual feature: it was transcendental. In mathematical terms, it means pi is not the root of any algebraic equation with rational coefficients. ... A life-long obsessive called William Shanks spent 20 years calculating pi to 707 decimal places. Unfortunately, his achievement was discredited when the first digital computers found that he had made a mistake at the 528th decimal place - rendering all subsequent digits meaningless. . ... [There is a lesson in poor Shanks' making a mistake, not realising it was a mistake, and thereafter unwittingly wasting his life working out the consequences of that mistake.

It is simply false the oft-repeated claim by so-called `sceptics', that the Bible in 1 Kings 7:23 (and in the parallel passage 2 Chronicles 4:2):

"He [Huram ... a man of Tyre and a craftsman in bronze] made the Sea of cast metal, circular in shape, measuring ten cubits from rim to rim and five cubits high. It took a line of thirty cubits to measure around it."

claims that the value of "PI is exactly 3":

"In I Kings 7:23, an altar font in Solomon's Temple was ten cubits across and thirty cubits around. This means that the mathematical constant PI (pi) is exactly 3. All school children know that PI is not 3 but 3.14159 and there is nothing to suggest that the Hebrew author was approximating. If PI is equal to exactly 3, then no machine, aeroplane, ship, motor vehicle etc. could be designed or would operate. The Bible's mathematics is consistent and in II Chronicles 4:2, we also read that PI is exactly 3. There are only two possible alternatives. Either the Bible is wrong and that PI is equal to 3.14159 or that the biblical PI is only approximate. Accordingly the Bible must be in error. Little wonder that many theologians argue that creationists who attempt to literally interpret the Bible mock the Bible, and by so mocking the Bible, they are anti-Christian. The creationist solution to the biblical approximation to the value of PI is to interpret only parts of the Bible as literal. A selective literal interpretation of the Bible is a common creationist contradiction." (Plimer I.R., "Telling lies for God," Random House: Sydney NSW, Australia, 1994, pp.17-18)

But the Bible makes no claim about the value of pi. It simply records that the circular basin built for Solomon's temple in fact measured "ten cubits from rim to rim and thirty cubits around it," a cubit being about 17.5 inches (or ~44.45 cm):

"The cubit was the distance from elbow to finger tip. ... This standard Hebrew cubit was 17.5 inches (44.45 cm), slightly shorter than the common Egyp. cubit of 17.6 inches (44.7 cm). This generally accepted figure compares closely with the length given for the Siloam tunnel as `1,200 cubits', equivalent to a measured 1,749 feet (533.1 m), giving a cubit of 17.49 inches or 44.42 cm. Excavated buildings at Megiddo, Lachish, Gezer and Hazor reveal a plan based on multiples of this measure. Also Solomon's bronze laver of 1,000 bath capacity (i.e. 22,000 litres; 1 Ki. 7:23-26; 2 Ch. 4:2, 5), when calculated for the capacity of a sphere, gives a cubit of 17.51 inches or 44.48 cm ." (Wiseman D.J., "Weights and Measures," in Douglas J.D., et al., eds., "New Bible Dictionary," [1962], Inter-Varsity Press, Leicester UK, Second edition, 1982, Reprinted, 1988, p.1247)

Now these were whole numbers, rounded to the nearest ten. So if the basin was a simple cylinder with actual dimensions of (say) diameter 9.7 and circumference 30.4 cubits, then the nearest whole numbers are 10 and 30, yet that is a ratio to the third decimal place (which neither the Hebrews then in ~970 BC, or anyone, had) of ~3.134, which is 0.008 (i.e. 8 thousandths) different from pi (3.142). Also, pi itself is an approximation - it is not as though there was an exact number of pi that the Bible got wrong. So there is no need to go any further. To the nearest whole number pi is in fact 3 and the Bible account is only concerned here with measurements to the nearest whole number (indeed, to the nearest multiple of ten).

But in fact, by considering what else the passage says about this basin in 1 Kings 7:24-26:

²³He made the Sea of cast metal, circular in shape, measuring ten cubits from rim to rim and five cubits high. It took a line of thirty cubits to measure around it. ²⁴Below the rim, gourds encircled it-ten to a cubit. The gourds were cast in two rows in one piece with the Sea. ²⁵The Sea stood on twelve bulls, three facing north, three facing west, three facing south and three facing east. The Sea rested on top of them, and their hindquarters were toward the center. ²⁶It was a handbreadth in thickness, and its rim was like the rim of a cup, like a lily blossom. It held two thousand baths.

it "was a handbreadth in thickness" and it had a "rim" that turned out "like the rim of a cup, like a lily blossom." A "handbreadth" (or palm) was one-sixth of a cubit:

"The long or `royal' cubit was a handbreadth (`palm') longer than the standard cubit of 6 palms (Ezk. 40:5), i.e. 20.4 inches or 51.81 cm. With this compare the Babylonian cubit of 50.3 cm (of 30 fingers length marked on a statue of Gudea) which was `3 fingers' shorter than the Egyp. cubit of 52.45 cm (Herodotus, Hist. 1. 178). ... The palm (tepah; topah) or `handbreadth' was the width of the hand at the base of the 4 fingers (hence Vulg. quattuor digitis), i.e. 7.37 cm. Thus was measured the thickness of the bronze laver (I Ki. 7:26 = 2 Ch. 4:5), the edge of the tabernacle table (Ex. 25:25; 37:12), and of that in Ezekiel's Temple (40:5; 43:13). A man's life is but (a few) handbreadths in length (Ps. 39:5)." (Wiseman, Ibid., p.1247).

Now if: 1) the width of the cup-like rim was a "handbreadth", i.e. the same as the thickness of the wall of the basin; 2) the diameter "measuring ten cubits from rim to rim" was taken from the outer edge of the cup-like rim; and 3) the circumference measurement of "a line of thirty cubits around it") was taken was around the main body of the basin; all of which is entirely reasonable, then the actual dimensions (using cubits because there is no need to convert it into modern units-the result is the same) of the main cylindrical body of the basin would be: a) diameter 10 cubits, less two handbreadths of 1/6th each, i.e. 10 - 1/3 = 9 2/3 = 9.67 cubits; and b) circumference of 30 cubits. That yields a ratio of 30/9.67 = 3.102, which is only 0.04 (i.e. four hundredths) less than pi (3.142), again to the third decimal place.

There are in fact other ways to reconcile the measurements of this basin with pi (and I have posted some of them on various Internet forums, e.g. June 4, 2000 & May 3, 2005), but they usually rely on the inside circumference of the basin being measured, which on reconsideration I find less plausible. I regard this solution (which is my own-as far as I am aware) to be more plausible.

Later note: Yesterday (17 March 2006), I was in a Christian bookstore and I saw a commentary on 1 and 2 Kings, which I had never read before. I opened it at 1 Kings 7:23 to see what it said about the dimensions of the basin and about pi. It said nothing about pi, but it did 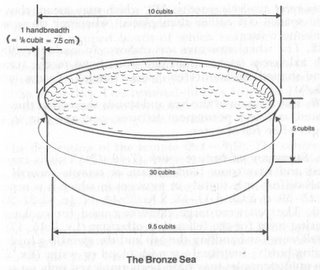have a drawing of the basin, which agrees with my proposal, except it makes a small mistake in giving the diameter of its cylinder body as 9.5 cubits, when 10 - (2 x 1/6) = 9 2/3 or 9.67 cubits. Indeed, that it did not even mention pi is evidence that that really is the best dimensions and measurements of the basin, independent of any question about pi. I also had since realised that being a casting, the width of the cup-like rim would almost certainly be a flared-out continuation of the thickness of the main body wall, which was 1/6th of a cubit (see above). Here is what the commentary said about this passage:

"1 KINGS 7:19-26 ... `The Bronze Sea' (7:23-26). This huge basin or reservoir was one of the great Hebrew technical works, corresponding in modern metallurgy to the casting of the largest church bell. It was viewed as a large expanse and volume of water (Heb. yam, `sea' is only used figuratively here, v. 23) and corresponded with the bronze basin in the tabernacle (Ex. 30:17-21). It was used by priests for cleansing their hands and feet and perhaps also to supply water to the standing basins for the rinsing of offerings (2 Ch. 4:10).
23. The size is given as five metres in diameter and two and a half metres in height and a handbreadth (v. 26, a sixth of a cubit = 7.5 cm.) thick. The capacity was about ten thousand gallons (two thousand baths is a measure, cf. the post-exilic `three thousand', 2 Ch. 4:5). [The bath is attested archaeologically as varying locally between 18 and 45 litres.] Its form has been reconstructed with the circumference given generally as thirty cubits." (Wiseman D.J., "1 and 2 Kings: An Introduction and Commentary," Tyndale Old Testament Commentaries," [1993], InterVarsity Press: Leicester UK, Reprinted, 2003, p.115)]

Stephen E. Jones, BSc. (Biol).
"Problems of Evolution"

---

"The difficulties which appear to oppose themselves to the reception of `Natural Selection' or `the survival of the fittest,' as the one explanation of the origin of species, have no doubt been already considered by Mr. Darwin. Nevertheless, it may be worth while to enumerate them, and to state the considerations which appear to give them weight; and there is no doubt but that a naturalist so candid and careful as the author of the theory in question, will feel obliged, rather than the reverse, by the suggestion of al the difficulties which can be brought against it. What is to be brought forward may be summed up as follows: That `Natural Selection' is incompetent to account for the incipient stages of useful structures. That it does not harmonize with the co-existence of closely similar structures of diverse origin. That there are grounds for thinking that specific differences may be developed suddenly instead of gradually. That the opinion that species have definite though very different limits to their variability is still tenable. That certain fossil transitional forms are absent, which might have been expected to be present. That some facts of geographical distribution intensify other difficulties. That the objection drawn from the physiological difference between `species' and `races' still exists unrefuted. That there are many remarkable phenomena in organic forms upon which `Natural Selection' throws no light whatever, but the explanations of which, if they could be attained, might throw light upon specific origination." (Mivart S.J., "On the Genesis of Species," Macmillan & Co: London & New York, Second edition, 1871, pp.24-25)